So you know about even and odd numbers. Even are those which can be divided by 2 without remainder, while the odd can't. What do you think 0 is? An odd or an even number? Well it cannot be divided by 2, but it is considered to be an even number - can you think of any explanation as to why?

There are several interesting facts about odd and even numbers. You can recognise them easily as all odd numbers, however big, end with an odd digit, while all even numbers end in an even digit (0, 2, 4,   6, 8).

There is only one prime number that is even. Which one is that?

As you already know, Pythagoreans were very interested in numbers. Among them, they were interested in even and odd numbers. Philolaus, a philosopher who wrote about Pythagoreans, and was a witness to their prosecution in Crotone (in Calabria, southern Italy - just opposite Sicily) wrote about numbers.

He actually made distinction between odd and even, and even-odd. Odd and even really are what we know that they are - but the even-odd number is a product of an even and an odd number.

So 4 is even, because 4 = 2 x 2

8 is even, because 8 = 2 x 4

but 6 is even-odd because 6 = 2 x 3

Can you find some more even-odd numbers?

Pythagoreans thought that all numbers can be represented geometrically and vice versa (until one unhappy afternoon). So they tried to represent even and odd numbers. Here are some possible representations of evens and odds:

an even number can be represented like this

Whilst an odd number can be represented like this

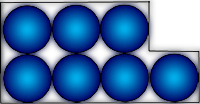
If you add two odd numbers you get...

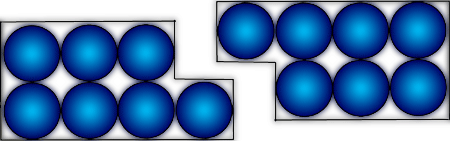
What would you get if you added two even-odd numbers? Investigate for yourself and see what happens with various odds and evens and even-odds.