imaginary

Imaginary numbers

home | courses | topics | theorems | starters | worksheets | timeline | KS3 | KS4 | KS5

Ok, let's get started with the real numbers: find the square roots of 9 and 25.

We usually write that as

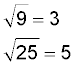
But are you really sure? What about (-3) as a solution to the first question, and (-5) as a solution to the second?

You should really always include the negative as one of the possible solutions to problems like these. Two negative numbers, when multiplied give positive, so no wonder that we didn't get -9 or -25, but the solutions could still be -3 and -5. The solutions to questions should then be

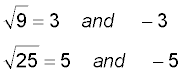
But what if we DO get a question such as finding a square root of -9? Then we have a problem on our hands - the square number is obtained by multiplying of a number by itself. So even if we imagine two negative numbers multiplying themselves the result would be positive.

Although this may be confusing to you (and not only to you, but it was confusing to many mathematicians over many centuries) eventually people came up with the idea of solving the problem by introducing an imaginary number. Euler seems to be the first person to name this imaginary number - in a paper he presented on May 5, 1777 to the Academy of St. Petersburg (but which was published only after his death in "Institutionum calculi integralis," (second ed., vol. 4, pp. 183-194, Impensis Academiae Imperialis Scientiarum, Petropoli, 1794) Euler says that we may imagine such a number which, when multiplied by itself gives -1.

So the imaginary number i is such that

Once imaginary numbers were defined, nothing could stop the complex numbers to come out and confuse eveyone!

See some pretty crazy - or even permanently irrational numbers here.

Or if you feel a bit crazy yourself, why don't you climb up the maths tree and see what branch you end up on.

Learn about Euler, and maybe even where he lived...

_____________________________________________________________________________________________________________________

Acknowledgements | Copyright | Contact | Mission Statement | Tell a friend about this site