Complex numbers
home | courses | topics | theorems | starters | worksheets | timeline | KS3 | KS4 | KS5
Complex numbers are very interesting creatures. They have two parts, one real and one imaginary. So real is just an ordinary number; imaginary is a bit different.
Complex numbers were discovered as people started looking into all the possible solutions to the equation. So some of the solutions were real numbers, some irrational, and some were imaginary or contained an 'imaginary' part.
Every complex number looks like this
where a is a real part, b is also a real number, but i is the imaginary number
Set of all complex numbers is denoted by 
; and it contains real numbers (denoted by 
). That is because you can imagine (!) that every real number has the imaginary part multiplied by 0:
As with other important mathematical discoveries, this one was not just the work of one man, but of many contributors. Mathematicians worked on understanding and defining complex numbers for a long time, but intensively from the 17th through to the 19th century. The acceptance of complex numbers did not really come until someone thought of a way to represent them geometrically.
Wallis, an English mathematician, had an idea how to represent complex numbers geometrically as early as 1685.
Wessel, a less known German mathematician, worked on this at the end of 18th century. This study was then taken by a better known German - Gauss, in 19th century.
So how do we represent them now? Here is a diagram to show you:
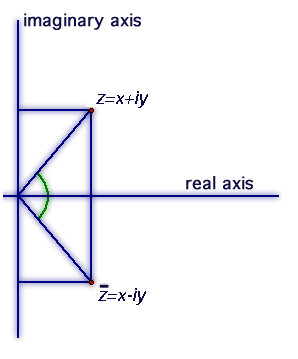
This diagram is actually known as Argand diagram, after a French mathematician (who was actually a bookseller), who published the idea in 1806, in Paris.
Why are complex numbers important? Find out from the story about the Fundamental Theorem of Algebra.
Click on the abacus to see some amazing mathematical artefacts.
John Wallis, 1616-1703
artefacts | numerals | concepts | people | places | pythagoreans | egyptians | babylonians
_____________________________________________________________________________________________________________________
Acknowledgements | Copyright | Contact | Mission Statement | Tell a friend about this site