coordinate geometry explanation

Explanation for the coordinate geometry of a straight line

home | courses | topics | theorems | starters | worksheets | timeline | KS3 | KS4 | KS5

Every straight line can be represented algebraically in the form y = mx + c , where

m represents the gradient of a line (its slope, steepness)

c represents the y -intercept (a point where the line crosses the y axis)

Furthermore, there are several ways in which you can describe a straight line algebraically

Equation of a line

	Line gradient m , the intercept on y -axis is c
	Line gradient m , passes through the origin
	Line gradient 1, makes an angle of 45 0 with the x -axis, and the intercept on the y axis is c
	Line is parallel to the x axis, through (0, k)
	Line is the x axis
	Line is parallel to the y axis, through ( k , 0)
	Line is the y axis
	General form of the equation of a straight line

The gradient measures the steepness of the line.

It is defined as , or

When the gradient is 1, the line makes a 45 0 angle with either axes. If the gradient is 0, the line is parallel to the x axis.

Equation of a straight line given the gradient and a point

If the point is given by its coordinates , and the gradient of a line is given as m , you can deduce the equation of that line.

You are using the formula for gradient, , to derive a formula for the line itself. The coordinates of the point can be substituted, while the y 2 and x 2 need to remain (without the superscript numbers).

Then simply substitute the given values into

The equation of a line given two points

When you have this kind of problem, you take that, as both points belong to the same line, the gradients at both points will be the same.

It makes sense therefore to say that

All you need to do in this case will be to substitute coordinates you have for the given points and .

Parallel and perpendicular lines

When two lines are parallel, their gradient is the same:

When two lines are perpendicular, their product equals -1: .

The line length

The length of the line segment joining two points will relate to their coordinates. Have a good look at the diagram

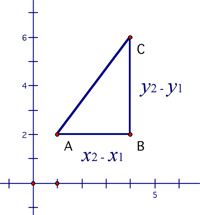
The length joining the point A and C can be found by using Pythagoras' Theorem:

Mid-point of a line

Mid-point of the line can be found by using the same principle

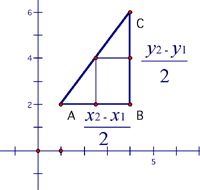
So the point between A and C will have the coordinates

If you know the midpoint, you can easily find the perpendicular bisector of a given line. This new line will go through the midpoint of the given line, and it will be perpendicular to it.

Have a look at the full list of topics for AS level maths

Download the booklet Coordinate geometry 1

or see the full list of resources for AS maths

See the history of coordinate geometry

Learn about Descartes by clicking on his portrait

_____________________________________________________________________________________________________________________

Acknowledgements | Copyright | Contact | Mission Statement | Tell a friend about this site