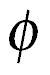is an irrational number. It doesn't end, it cannot be expressed as a fraction of two integers, and it can be found in many places both in nature and in art. It is closely linked to the famous Fibonacci Number Sequence.

Fibonacci's numbers have a curious property: if you divide them in succession with the previous numbers in the sequence, the result approximates closer and closer to the number

= 1.6180339887...

Fibonacci Number sequence is a sequence which looks like this:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55...

Funny thing is - number is equal to the ratio that you can find in the Golden Section. Golden Section, or Ratio, or Mean, has been known to the ancient Greeks. In fact the number probably got its name from Phidias (in Greek would be Phi), a famous Athenian sculptor who often used the Golden Section proportions in his work. Golden Section was also described in Euclid's Elements in few places   - and here is another little task for you - find all theorems that refer to it! Here is how Golden Ratio is described by Euclid:

A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.

Let us think carefully what this means. You need to divide the line in such a way that the bigger part of it is to the whole line in the same ratio as the smaller is to the bigger part. Geometrically this should look like the following diagram:

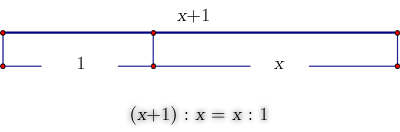
You can now download the worksheet which will help you learn how to construct Golden Ratio and how you can use it to draw Golden Rectangle and the logarithmic spiral.