polynomials

Polynomials, their degree and their roots

home | courses | topics | theorems | starters | worksheets | timeline | KS3 | KS4 | KS5

Polynomials

Polynomials are expressions which are made up of constants and variables in any order, but only using addition, subtraction and multiplication (not division or anything else!).

So for example

is a polynomial

but

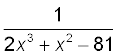is not a polynomial.

Roots

If you equate the polynomial with 0, then you get an equation:

To solve equations in which highest power of x is 2, you can use the formula

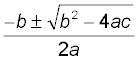
where a, b and c are the coefficients next to the variable (a next to the squared x, b next to x, c on its own). The solutions to this equation will be its roots.

For the example given above, roots are

x = -1 and x = 5

You can then write your polynomial as a product of

(x+1)(x-5)=0

Degree of a polynomial

The highest power of the variable in the polynomial determines its degree. So the polynomial

is of a second degree because that is the highest degree of a variable, whereas the polynomial of

is of a third degree, as that is the highest degree of a variable in that polynomial.

The Fundamental Theorem of Algebra is very much related to polynomials. Click here to learn more about it .

You can also learn about other theorems and conjectures here.

Or climb the mathematical tree and see what branch you end up on.

_____________________________________________________________________________________________________________________

Acknowledgements | Copyright | Contact | Mission Statement | Tell a friend about this site