
Completing the Square - how to do it
home | courses | topics | theorems | starters | worksheets | timeline | KS3 | KS4 | KS5
A very nice way of solving quadratic equations is through 'completing the square'. It is nice because it is a relatively easy method, and it also gives you some information about the graph of the quadratic in question.
Perfect Squares are expressions such as these:
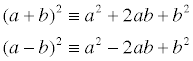
Every quadratic expression can be written as
![]()
Let's say you have a usual quadratic of the form
![]() , where
, where ![]()
You need to use half of b , so let us introduce a value p such that 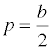 .
.
Re-write your equation as
![]()
Because neither p 2 nor c have x 'attached' to them, you can tidy the equation up and that will be the completed square of the original equation.
You can also use the completed square form to sketch the graph of a quadratic faster. The information given by the completed square form is
![]()
This is useful not only for finding the zeros (roots) of the quadratic, but also because you can then easily sketch it.
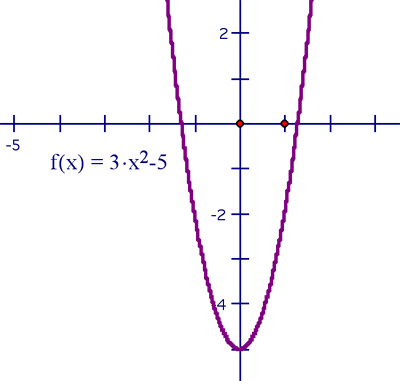
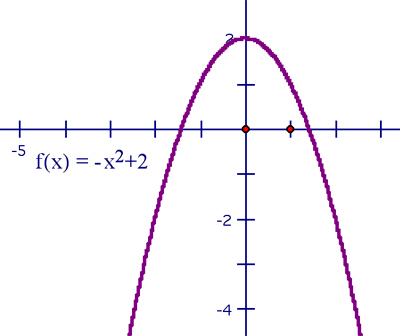
The vertex of parabola will have coordinates (- p,q ); its axis of symmetry will be x = -p . It will be U (valley) shaped if a > 0, and 'hill' shaped if a < 0.
a > 0
a < 0
artefacts | numerals | concepts | people | places | pythagoreans | egyptians | babylonians
_____________________________________________________________________________________________________________________
Acknowledgements | Copyright | Contact | Mission Statement | Tell a friend about this site